5.4.1. 算术和逻辑电路
算术和逻辑电路实现 ISA 的算术和逻辑指令,它们共同构成了处理器的算术逻辑单元 (ALU)。算术和逻辑电路还实现 CPU 中其他功能的部分。例如,算术电路用于增加程序计数器 (PC) 作为指令执行的第一步,并且它们用于通过组合指令操作数位和寄存器值来计算内存地址。
电路设计通常从使用逻辑门实现简单电路的 1 位版本开始。然后,将此 1 位电路用作实现 M 位版本电路的构建块。使用基本逻辑门设计 1 位电路的步骤如下:
- 设计电路的真值表:确定输入和输出的数量,并为指定输出位的值的每个输入位排列添加一个表条目。
- 使用真值表,根据每个电路的输入值与“AND”、“OR”、“NOT”的组合,写出当每个电路的输出为 1 时的表达式。
- 将表达式转换成一系列逻辑门,其中每个门从电路的输入或前一个逻辑门的输出获取输入。
我们按照以下步骤实现单比特相等电路:当A和B的值相同时,按位相等(A == B)输出 1,否则输出 0。
首先,设计电路的真值表:
表 1. 简单相等电路的真值表
| A | B | A == B output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
接下来,用 AND、OR 和 NOT 结合A和B写出A == B为 1 时的表达式。首先,分别考虑输出为 1 的每一行,从真值表的第一行开始:
| A | B | A == B |
|---|---|---|
| 0 | 0 | 1 |
对于此行中的输入值,构造一个由其输入的表达式组成的 连接词,其计算结果为 1。连接词将计算结果为 0 或 1 的子表达式与 AND 结合在一起,并且仅当两个子表达式的计算结果都为 1 时,其本身才为 1。首先表达每个输入计算结果为 1 的情况:
NOT(A) # is 1 when A is 0
NOT(B) # is 1 when B is 0
然后,创建它们的合取(用 AND 将它们结合起来)以得出当真值表的这一行计算结果为 1 时的表达式:
NOT(A) AND NOT(B) # is 1 when A and B are both 0
我们对真值表的最后一行执行同样的事情,其输出也是 1:
| A | B | A == B |
|---|---|---|
| 1 | 1 | 1 |
A AND B # is 1 when A and B are both 1
最后,对真值表中计算结果为 1 的行对应的每个合取运算创建一个析取(disjunction, 或):
(NOT(A) AND NOT(B)) OR (A AND B) # is 1 when A and B are both 0 or both 1
此时,我们有一个可以转换为电路的表达式A == B。在此步骤中,电路设计人员采用技术简化表达式以创建最小等效表达式(对应于电路中最少的运算符和/或最短门路径长度的表达式)。设计人员在最小化电路设计时必须非常小心,以确保转换后的表达式的等价性。有一些用于电路最小化的正式方法超出了我们的范围,但我们在开发电路时会采用一些启发式方法。
在我们的例子中,我们直接将前面的表达式转换为电路。我们可能想用 (A NAND B) 替换 (NOT(A) AND NOT(B)),但请注意,这两个表达式 并不 等价:它们对 A 和 B 的所有排列的求值并不相同。例如,当 A 为 1 且 B 为 0 时,(A == B) 为 0 且 (A NAND B) 为 1。
要将表达式转换为电路,请从最内层的表达式开始并向外工作(最内层将是第一个门,其输出将是后续门的输入)。第一组门对应于输入值的任何否定(输入 A 和 B 的非门)。接下来,对于每个合取,创建电路的各个部分,将输入值输入到与门中。然后将与门输出输入到表示分离的或门中。结果电路如 图 1 所示。

图 1. 由 AND、OR 和非逻辑门构成的 1 位相等电路(A == B)。
为了验证该电路的正确性,请模拟输入值 A 和 B 通过电路的所有可能排列,并验证电路的输出是否与真值表中 (A == B) 的对应行匹配。例如,如果 A 为 0 且 B 为 0,则两个非门在馈入顶部与门之前会对其值求反,因此此与门的输入为 (1, 1),从而导致输出为 1,这是或门的顶部输入值。A 和 B 的值 (0, 0) 直接馈入底部与门,导致底部与门输出 0,这是或门的下部输入。因此,或门接收输入值 (1, 0) 并输出值 1。因此,当 A 和 B 都为 0 时,电路正确输出 1。图 2 说明了这一示例。
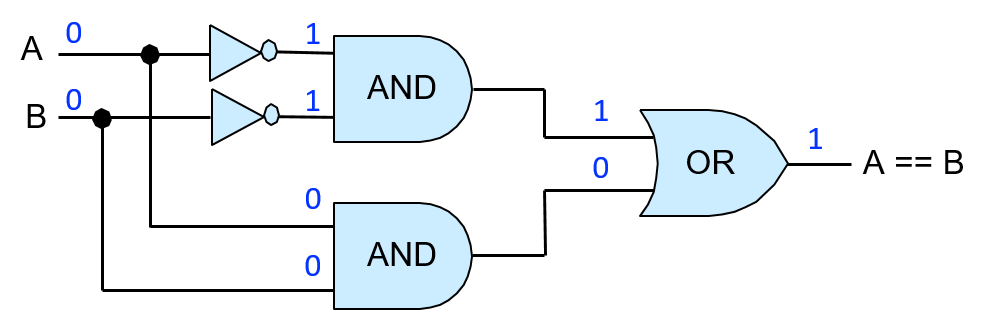
图 2. 示例显示 1 位相等电路如何计算 (A == B)。从 A 的输入值 0 和 B 的输入值 0 开始,这些值通过组成电路的门传播,以计算出 A == B 的正确输出值 1。
将 1 位相等电路的实现视为一个单元,可以将其从实现中抽象出来,从而可以更轻松地将其用作其他电路的构建块。我们将 1 位相等电路的这个抽象(如图 3 所示)表示为一个框,其两个输入标记为 A 和 B,单个输出标记为 A == B。实现 1 位相等电路的内部门隐藏在电路的这个抽象视图中。
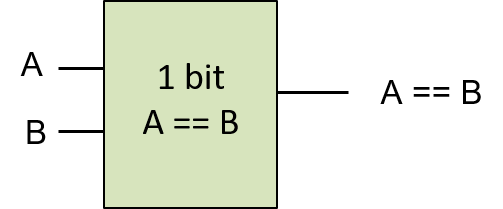
图 3. 1 位相等电路抽象。该电路可用作其他电路的构建块。
单位版本的 NAND、NOR 和 XOR 电路可以类似地构建,仅使用 AND、OR 和 NOT 门,从它们的真值表 (表 2) 开始,并应用与 1 位相等电路相同的步骤。
表 2. NAND、NOR 和 XOR 电路的真值表。
| A | B | A NAND B | A NOR B | A XOR B |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
这些电路的多位版本是由多个单位版本电路构成的,其构成方式类似于 4 位 AND 门由四个 1 位 AND 门构成的。
算术电路
算术电路的构造方法与构造逻辑电路的方法完全相同。例如,要构造 1 位加法器电路,请从单比特加法的真值表开始,该表具有两个输入值 A 和 B,以及两个输出值,一个用于 A 与 B 的总和,另一个输出用于溢出或进位。表 3 显示了 1 位加法的结果真值表。
表 3. 1 位加法器电路的真值表。
| A | B | SUM | CARRY OUT |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
在下一步中,对于每个输出 SUM 和 CARRY OUT,创建输出值为 1 时的逻辑表达式。这些表达式表示为输入值的每行连接的析取:
SUM: (NOT(A) AND B) OR (A AND NOT(B)) # 1 when exactly one of A or B is 1
CARRY OUT: A AND B # 1 when both A and B are 1
CARRY OUT 的表达式无法简化。但是,SUM 的表达式更复杂,可以简化,从而简化电路设计。首先要注意的是,SUM 输出也可以表示为 (A XOR B)。如果我们有一个 XOR 门或电路,将 SUM 表示为 (A XOR B) 会导致加法器电路设计更简单。如果没有,则使用 AND、OR 和 NOT 的表达式,并使用 AND、OR 和 NOT 门来实现。
假设我们有一个 XOR 门,可用于实现 1 位加法器电路。结果电路如 图 4 所示。
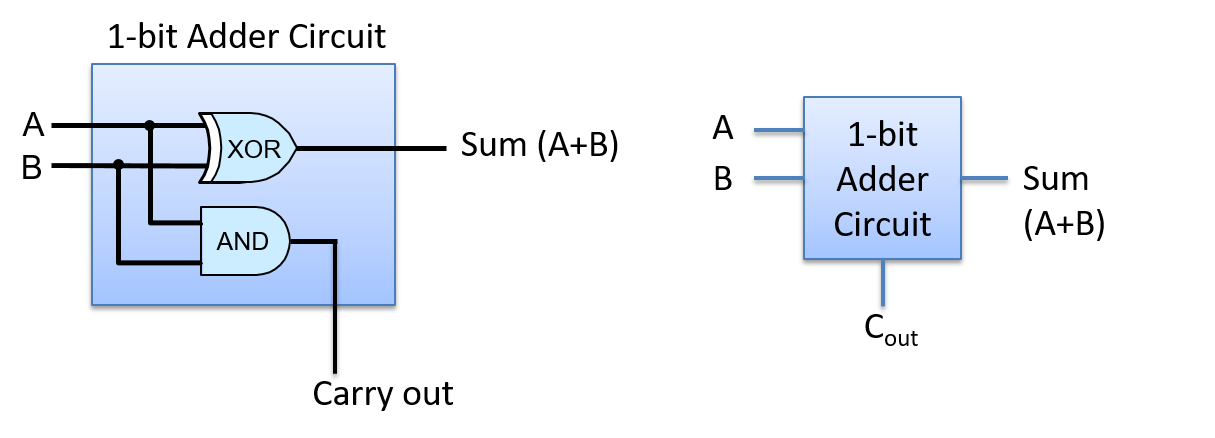
图 4. 1 位加法器电路有两个输入,A 和 B,以及两个输出,SUM 和 CARRY OUT。
1 位加法器电路可用作更复杂电路的构建块。例如,我们可能想要创建 N 位加法器电路来对不同大小的值执行加法(例如 1 字节、2 字节或 4 字节加法器电路)。但是,从 N 个 1 位加法器电路创建 N 位加法器电路比从 N 个 1 位逻辑电路创建 N 位逻辑电路需要更加小心。
执行多位加法(或减法)时,各个位按从最低有效位到最高有效位的顺序相加。在进行此按位加法时,如果第 i 位之和的进位值为 1,则将两个第 (i+1) 位加上一个额外的 1。换句话说,第 i 位加法器电路的进位是第 (i+1) 位加法器电路的输入值。
因此,要实现多位加法器电路,我们需要一个新的 1 位加法器电路,该电路具有三个输入:A、B 和 CARRY IN。为此,请按照上述步骤创建一个 1 位加法器电路,该电路具有三个输入(A、B、CARRY IN)和两个输出(SUM 和 CARRY OUT),从其三个输入的所有可能排列的真值表开始。我们将这个电路的设计留给读者作为练习,但我们在 图 5 中展示了它作为 1 位加法器电路的抽象。
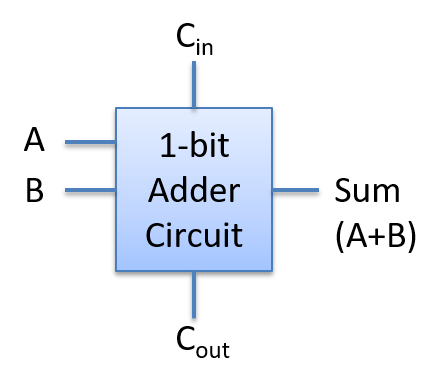
图 5. 具有三个输入(A、B 和 CARRY IN)和两个输出(SUM 和 CARRY OUT)的 1 位加法器电路。
用此版本的 1 位加法器电路作为构建块,我们可以通过将相应的操作数位馈送到单独的 1 位加法器电路来构建 N 位加法器电路,将第 i 个 1 位加法器电路的 CARRY OUT 值馈送到第 _(i+1) 个 1 位加法器电路的 CARRY IN 值中。第 0 位的 1 位加法器电路从解码 ADD 指令的 CPU 电路的另一部分接收其 CARRY IN 的值 0。
这种由 N 个 1 位加法器电路构成的 N 位加法器电路称为行波进位加法器,如图 6 所示。SUM 结果在电路中从低位到高位进行波纹传播。只有在计算 SUM 和 CARRY OUT 值的第 0 位之后,SUM 和 CARRY OUT 的第 1 位才能正确计算。这是因为第 1 位的 CARRY IN 从第 0 位的 CARRY OUT 获取其值,结果的后续高位亦然。
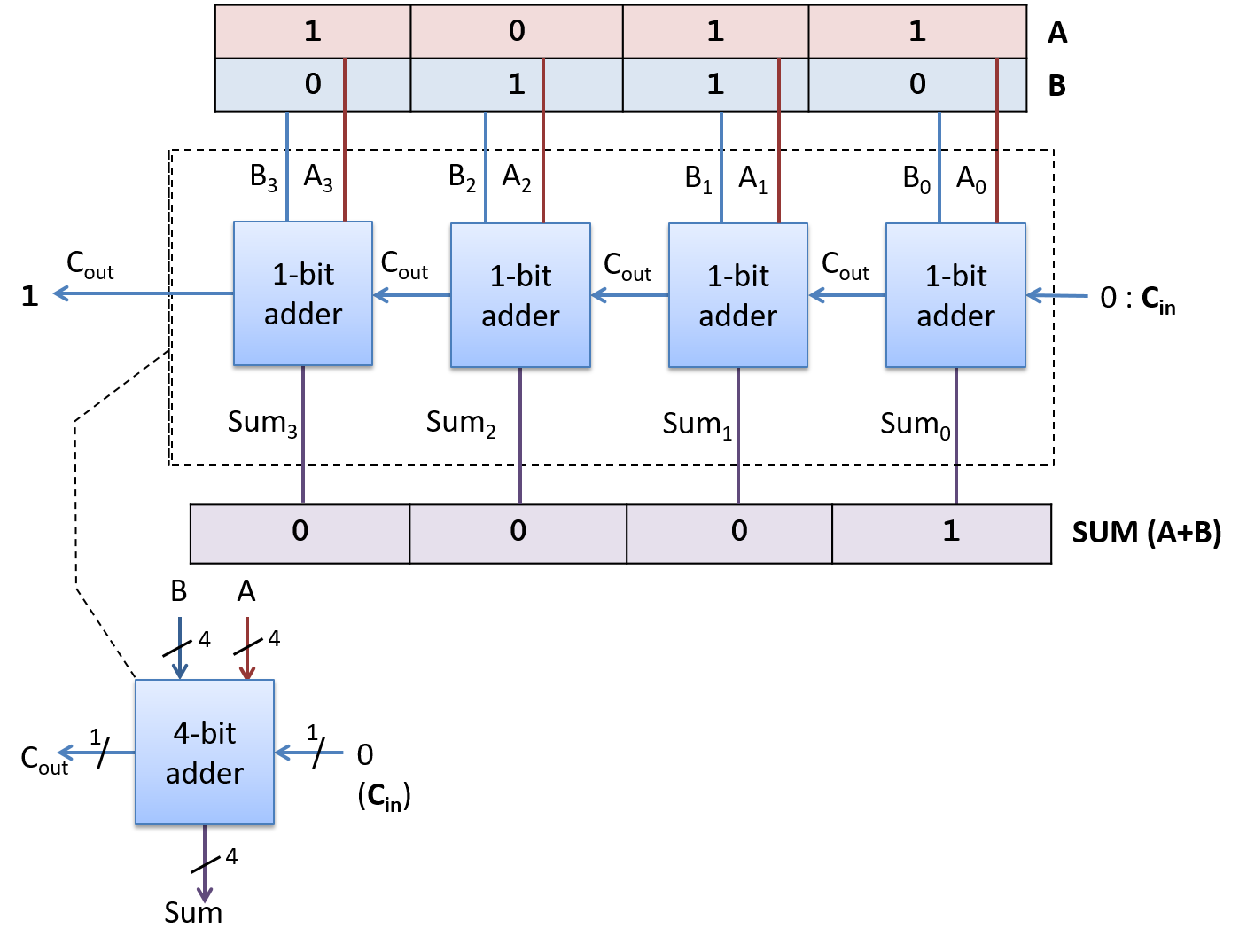
图 6. 由四个 1 位加法器电路创建的 4 位波纹加法器电路。
其他算术和逻辑功能的电路也是通过组合电路和逻辑门以类似的方式构建的。例如,计算 (A - B) 的减法电路可以由计算减法 (A + (-B)) 的加法器和求反电路构建而成。